It is seen that in many waveform, some of these does not have sine terms,some of dose not contain cosine terms. Also in some other harmonics are found missing. This is because of certain types of symmetry associated with the waveforms, which results in some Fourier coefficient being absent from the series.
Following symmetries are considered:
- Odd or rotation symmetry
- Even or mirror symmetry
- Half wave or alternation symmetry
- Quarter wave symmetry
1.ODD SYMMETRY:
A function is said to be odd if,
[tex]f(x) = - f( - x)[/tex]
[tex]\sin x = x - \frac{{{x^3}}}{{3!}} + \frac{{{x^5}}}{{5!}} - \frac{{{x^7}}}{{7!}} + ...[/tex]
obviously sinx is odd function.
2. EVEN SYMMETRY:
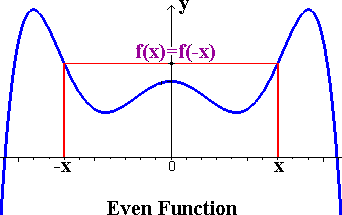A function is said to be even if,
[tex]f(x) = f( - x)[/tex]
[tex]\cos x = 1 - \frac{{{x^2}}}{{2!}} + \frac{{{x^4}}}{{4!}} - \frac{{{x^6}}}{{6!}} + ....[/tex]
hence cosx is an even function.
- 2125 views