Kirchhoff's Laws

Kirchhoff's laws simply deal with voltage drops and rises with the current flowing in a circuit by using the ideas of simple energy conservation. These laws are very helpful in determining of the output response for network analysis.

KIRCHHOFF'S LAW:

1. Kirchhoff's Voltage law(KVL): The algebraic sum of all branch voltages around any closed loop of a network is zero at all instants of time. 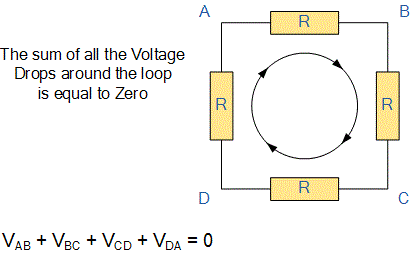                Mathematically kvl can be written as, $\sum {V = 0}$                                                                                                                                     
2. Kirchhoff's Current law(KCL): The algebraic sum of the branch currents at a node is zero at all instants of time.

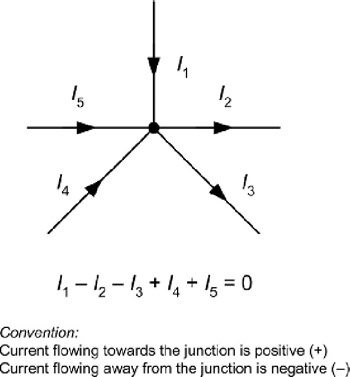
Mathematically kcl maybe written as, $\sum {i = 0}$

Based on KVL and KCL we can write the loop and node equations respectively.

Example: Let us take a circuit and referring the circuit node and loop equations are written,

                                                                   Node A                                      Node B

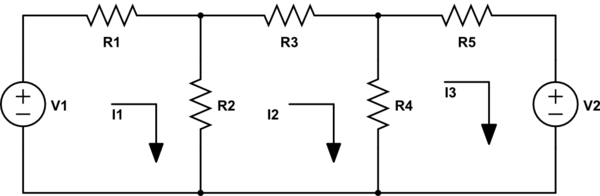
We have three loops and the currents in the elements are as specified. By KVL, we get

${I_1}{R_1} + ({I_1} - {I_2}){R_2} = {V_1}$

$({I_2} - {I_1}){R_2} + {I_2}{R_3} + ({I_2} - {I_3}){R_4} = 0$

$({I_3} - {I_2}){R_4} + {I_3}{R_5} = {V_2}$

Similarly using KCL,the node equations can be written as:

Taking voltage of node A is ${V_A}$ and voltage of node B is${V_B}$

$\frac{{({V_A} - {V_1})}}{{{R_1}}} + \frac{{{V_A}}}{{{R_2}}} + \frac{{({V_A} - {V_B})}}{{{R_3}}} = 0$

$\frac{{({V_B} - {V_A})}}{{{R_3}}} + \frac{{{V_B}}}{{{R_4}}} + \frac{{({V_B} - {V_2})}}{{{R_5}}} = 0$