D’Alembert’s Principle states that,
For any body, the algebraic sum of externally applied forces and the forces resisting motion in any given direction is zero.
This principle is obeyed by the static equilibrium of a dynamic system subjected to an external driving force.
In a translational mechanical system is subjected to an external force F , 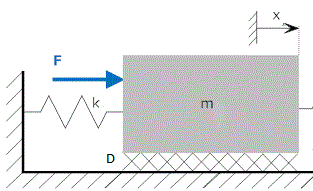
as shown we can write the equilibrium equation by D’Alembert’s Principle as
[tex]F + {F_M} + {F_D} + {F_K} = 0[/tex]
where,
1. Inertial force, [tex]{F_M} = - M\frac{{dx}}{{dt}}[/tex]
2. Damping force, [tex]{F_D} =- Dx[/tex]
3. Spring force, [tex]{F_K} = - \frac{1}{K}\int {udt} [/tex]
The direction of forces due to inertia, damping and spring are opposite to that of applied external force F.
Hence the equation becomes
[tex]F = M\frac{{dx}}{{dt}} + Dx + \frac{1}{K}\int {udt} [/tex]
For rotational system,D’Alembert’s Principle can be stated as,
For any body, the algebraic sum of externally applied torques and the torque resisting rotation about any axis is zero.
- 725 views






