A.C. Bridges for Measurement of Resistance, Inductance, Capacitance, Frequency etc.

Alternating current bridge methods are important for measurement of inductance, capacitance, storage factor, dissipation factor etc.The a.c. bridge is natural out growth of Wheatstone Bridge.It's basic form consist of four arms, a source of excitation(ac source), a balance detector.

 

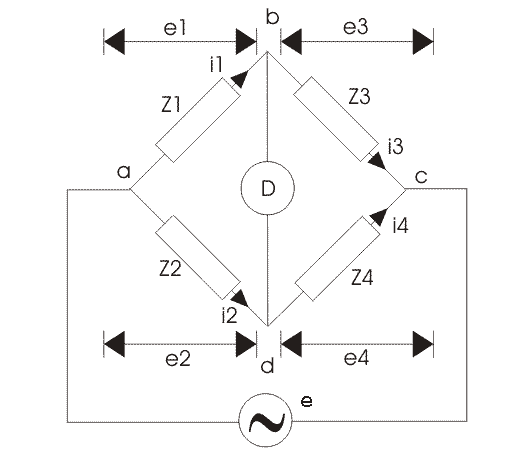GENERAL EQUATION FOR BRIDGE BALANCE

For balance of bridge the condition required is no current through the detector

i.e. the potential difference between points b and d should be zero. This is possible when,  ${e_1} = {e_2}$

                    or,${i_1}{z_1} = {i_2}{z_2}$            ......................(1)

Also at balance,

                       ${i_1} = {i_3} = \frac{e}{{{z_1} + {z_3}}}$     .......(2)

          and       ${i_2} = {i_4} = \frac{e}{{{z_2} + {z_4}}}$     ........(3)

substitute eqn.(2) and eqn.(3) gives,

                        ${z_1}{z_4} = {z_2}{z_3}$

This is the basic equation for balanced ac bridge.

Consider the polar form, the impedance can be written as,$z = z\angle \theta$. z represents magnitude and $\theta$represents the phase angle of the complex impedance.

Hence,            $({z_1}\angle {\theta _1})({z_4}\angle {\theta _4}) = ({z_2}\angle {\theta _2})({z_3}\angle {\theta _3})$

For balance,${z_1}{z_4}\angle ({\theta _1} + {\theta _4}) = {z_2}{z_3}\angle ({\theta _2} + {\theta _3})$

MEASUREMENT OF INDUCTANCE

MAXWELL'S INDUCTANCE BRIDGE:

This bridge is used to measure self-inductance by comparison with a variable standard self-inductance.

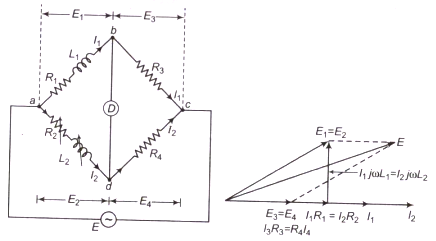
The connection of bridge and phasor diagram for balanced circuit is shown.

Here,

${L_1}$= inductance to be measured with resistance ${R_1}$

${L_2}$=variable inductance

${R_2}$=variable resistance

                                                                                                            ${R_3}$,${R_4}$= pure resistance

The balanced condition is that,       ${z_1}{z_4} = {z_2}{z_3}$

                                                  or,  $({R_1} + j\omega {L_1}){R_4} = ({R_2} + j\omega {L_2}){R_3}$

Equating real and imaginary part of both sides,

$$\begin{array}{l} {R_1}{R_4} = {R_2}{R_3}\\ {R_1} = \frac{{{R_2}{R_3}}}{{{R_4}}} \end{array}$$

and,

$$\begin{array}{l} {L_1}{R_4} = {L_2}{R_3}\\ {L_1} = \frac{{{L_2}{R_3}}}{{{R_4}}} \end{array}$$

Hence the unknown resistance can be measured in terms of known inductance and two resistors.And the whole process are independent of frequency. This bridge is used for measurement of iron losses of transformer at audio frequency.

MAXWELL,S INDUCTANCE CAPACITANCE BRIDGE:

Here, an inductance is measured by comparison with standard capacitance.

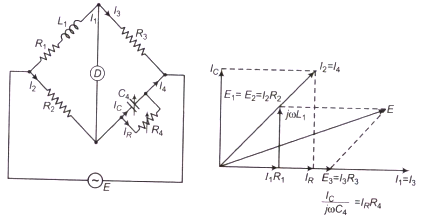
The connection of bridge and phasor diagram for balanced circuit is shown.

Here,

${L_1}$= inductance to be measured with resistance ${R_1}$

${R_2}$,${R_3}$,${R_4}$= are known pure resistance.

${C_4}$=variable standard capacitor.

Now,

$$\begin{array}{l} {Z_1} = \left( {{R_1} + j\omega {L_1}} \right);\\ {Z_2} = {R_2};\\ {Z_3} = {R_3};\\ {Z_4} = \frac{{{R_4}}}{{1 + j\omega {C_4}{R_4}}} \end{array}$$

The balanced condition is that,      

                                                                ${z_1}{z_4} = {z_2}{z_3}$

$$\begin{array}{l} \left( {{R_1} + j\omega {L_1}} \right)\left( {\frac{{{R_4}}}{{1 + j\omega {C_4}{R_4}}}} \right) = {R_2}{R_3}\\ {R_1}{R_4} + j\omega {L_1}{R_4} = {R_2}{R_3} + j\omega {R_2}{R_3}{C_4}{R_4} \end{array}$$

Equating real and imaginary part of both sides,

$$\begin{array}{l} {R_1} = \frac{{{R_2}{R_3}}}{{{R_4}}}\\ {L_1} = {R_2}{R_3}{C_4} \end{array}$$

Expression for Q factor,  $Q = \frac{{\omega {L_1}}}{{{R_1}}} = \omega {C_4}{R_4}$

HAY'S BRIDGE:

Hay's bridge is a modification of Maxwell's bridge with a series resistance connected to standard capacitor, instead of resistance parallel with capacitor.

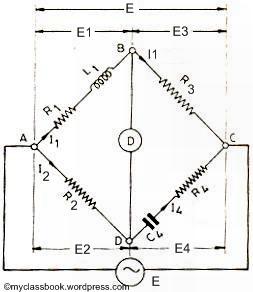
Let,

${L_1}$= inductance to be measured with resistance ${R_1}$

${R_2}$,${R_3}$,${R_4}$= are known pure resistance.

${C_4}$= Standard capacitor.

Now,

$$\begin{array}{l} {Z_1} = {R_1} + j\omega {L_1};\\ {Z_2} = {R_2};\\ {Z_3} = {R_3};\\ {Z_4} = {R_4} - \frac{j}{{\omega {C_4}}} \end{array}$$

The balanced condition is that,      

                                                    ${z_1}{z_4} = {z_2}{z_3}$

                                                or,$({R_1} + j\omega {L_1})\left( {{R_4} - \frac{j}{{\omega {C_4}}}} \right) = {R_2}{R_3}$

Separating real and imaginary terms,we get,

$$\begin{array}{l} {R_1}{R_4} + \frac{{{L_1}}}{{{C_4}}} = {R_2}{R_3}\\ {L_1} = \frac{{{R_1}}}{{{\omega ^2}{R_4}{C_4}}} \end{array}$$

Solving these simultaneous equations we get,

$$\begin{array}{l} {R_1} = \frac{{{\omega ^2}{R_2}{R_3}{R_4}C_4^2}}{{1 + {\omega ^2}R_4^2C_4^2}}\\ {L_1} = \frac{{{R_2}{R_3}{C_4}}}{{1 + {\omega ^2}R_4^2C_4^2}} \end{array}$$

The expressions contain the frequency term which is same as the frequency of source of supply.

Hence for calculation of unknown inductance we should know the frequency of supply.

ANDERSON'S BRIDGE:

This bridge is modification of the maxwell's inductance capacitance bridge. Here self inductance is measured in terms of standard capacitor over a wide range of values.

 

 

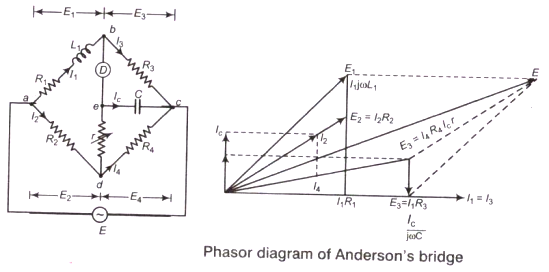
${L_1}$= the self-inductance to be measured

${R_1}$=resistance connected in series with self-inductor

${r}$,${R_2}$,${R_3}$,${R_4}$= are known pure resistance.

C= fixed standard capacitor.

At balance,

$\begin{array}{l} {I_1} = {I_3}\\ {I_2} = {I_c} + {I_4}\\ {I_1}{R_3} = {I_c} \times \frac{1}{{j\omega C}}\\ {I_c} = {I_1}j\omega C{R_3} \end{array}$

Writing the other balance eqations

${I_1}\left( {{R_1} + j\omega {L_1}} \right) = {I_2}{R_2} + {I_c}r$

${I_1}\left( {{R_1} + j\omega {L_1}} \right) = {I_2}{R_2} + {I_1}j\omega C{R_3}r$

${I_1}\left( {{R_1} + j\omega {L_1} - j\omega C{R_3}r} \right) = {I_2}{R_2}$     ..................................(1)

and

${I_c}\left( {r + \frac{1}{{j\omega C}}} \right) = \left( {{I_2} - {I_c}} \right){R_4}$

${I_1}j\omega C{R_3}\left( {r + \frac{1}{{j\omega C}}} \right) = \left( {{I_2} - {I_1}j\omega C{R_3}} \right){R_4}$

${I_1}\left( {j\omega C{R_3}r + {R_3} + j\omega C{R_3}{R_4}} \right) = {I_2}{R_4}$      ..........................(2)

From equation (1) and (2) we get

${I_1}\left( {j\omega C{R_3}r + {R_3} + j\omega C{R_3}{R_4}} \right) \times \frac{1}{{{R_4}}} = {I_1}\left( {{R_1} + j\omega {L_1} - j\omega C{R_3}r} \right) \times \frac{1}{{{R_2}}}$

Equating real and imaginary part,

$$\begin{array}{l} {R_1} = \frac{{{R_2}{R_3}}}{{{R_4}}}\\ {L_1} = \frac{{C{R_3}}}{{{R_4}}}\left[ {r\left( {{R_4} + {R_2}} \right) + {R_2}{R_4}} \right] \end{array}$$

This method is used for measurement over a wide range of values from few micro_henrys to several henrys.

OWEN'S BRIDGE:

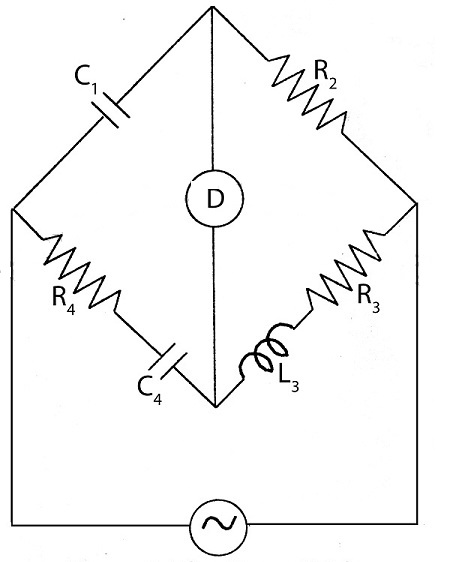  The circuit diagram of this bridge is shown. Here also unknown inductance is measured in terms of resistance and capacitance.

From figure,

$$\begin{array}{l} {Z_1} =  - \frac{j}{{\omega {C_1}}}\\ {Z_2} = {R_2}\\ {Z_3} = {R_3} + j\omega {L_3}\\ {Z_4} = {R_4} - \frac{j}{{\omega {C_4}}} \end{array}$$

Balance condition is,

${Z_1}{Z_3} = {Z_2}{Z_4}$

$- \frac{j}{{\omega {C_1}}}\left( {{R_3} + j\omega {L_3}} \right) = {R_2}\left( {{R_4} - \frac{j}{{\omega {C_4}}}} \right)$

By separating real and imaginaries, we get

$$\begin{array}{l} {R_3} = \frac{{{R_2}{C_1}}}{{{C_4}}}\\ {L_3} = {C_1}{R_2}{R_4} \end{array}$$

Here is no need of frequency in final balance equation. Hence bridge is unaffected by frequency variation and wave form.

MEASUREMENT OF CAPACITANCE

De SAUTY'S BRIDGE:

In this bridge it is simplest to measure capacitance by comparing two capacitor. With respect to figure,

${C_2}$=capacitor to be measured

${C_3}$=a standard capacitor

${R_1}$,${R_4}$= non-inductive resistor

By varying either ${R_4}$ or ${R_1}$

Let ${I_1}$ be current through ${R_1}$ and${C_2}$

and ${I_2}$ be current through ${R_4}$and${C_3}$

At balanced condition,

          ${I_1}{R_1} = {I_2}{R_4}$    .......................(1)

and,   ${I_1} \times \frac{{ - j}}{{\omega {C_2}}} = {I_2} \times \frac{{ - j}}{{\omega {C_3}}}$    .......................(2)

From the two equations we get,

           $\frac{{{R_1}}}{{{R_4}}} = \frac{{{C_2}}}{{{C_3}}}$

           ${C_2} = {C_3} \times \frac{{{R_1}}}{{{R_4}}}$

If both the capacitors not free from dielectric loss this bridge method will goes offset. A perfect balance occur if air capacitors are used.

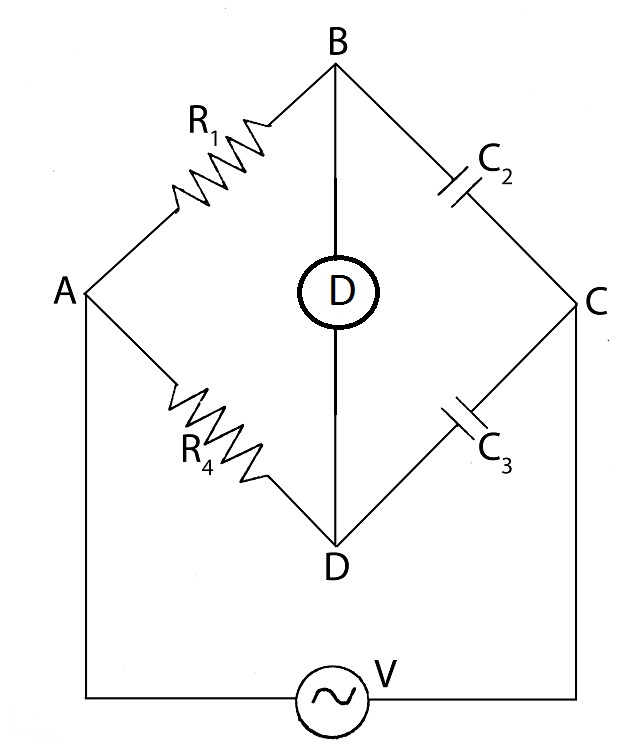
SCHERING BRIDGE:

${C_1}$=capacitor to be measured

${C_2}$=a standard capacitor

${R_3}$= non-inductive resistor

${R_4}$=variable non-inductive resistor

${C_2}$=variable capacitor

 

 

 

At balance,

$$\begin{array}{l} \left( {{r_1} + \frac{1}{{j\omega {C_1}}}} \right)\left( {\frac{{{R_4}}}{{1 + j\omega {C_4}{R_4}}}} \right) = \frac{{{R_3}}}{{j\omega {C_2}}}\\ \left( {{r_1} + \frac{1}{{j\omega {C_1}}}} \right){R_4} = \frac{{{R_3}}}{{j\omega {C_2}}}\left( {1 + j\omega {C_4}{R_4}} \right) \end{array}$$

Equating real and imaginary part,

$$\begin{array}{l} {r_1} = \frac{{{R_3}{C_4}}}{{{C_2}}}\\ {C_1} = {C_2}\left( {\frac{{{R_4}}}{{{R_3}}}} \right) \end{array}$$

MEASUREMENT OF FREQUENCY

WIEN'S BRIDGE:

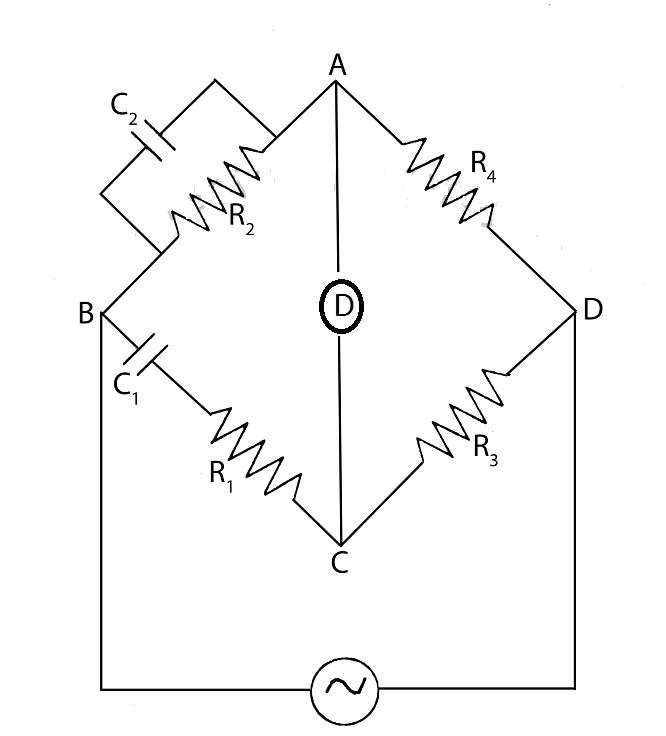The bridge circuit is shown in figure. The usual balanced relationship gives,

${R_4}\left( {{R_1} - \frac{j}{{\omega {C_1}}}} \right) = {R_3}\left( {\frac{{{R_2}}}{{1 + j\omega {C_2}{R_2}}}} \right)$

Separating real and imaginary part,

$$\begin{array}{l} {R_1}{R_4} + {R_2}{R_4}\frac{{{C_2}}}{{{C_1}}} = {R_2}{R_3}\\ \frac{{{C_2}}}{{{C_1}}} = \frac{{{R_3}}}{{{R_4}}} - \frac{{{R_1}}}{{{R_2}}} \end{array}$$

 

 

And,

$$\begin{array}{l} \omega {C_2}{R_2}{R_4} - \frac{{{R_4}}}{{\omega {C_1}}} = 0\\ {\omega ^2} = \frac{1}{{{C_1}{C_2}{R_2}{R_4}}} \end{array}$$

Wien's bridge also had applications on audio and HF oscillators as the frequency determining device.